Clustering
데이터 instance들을 비슷한 것끼리 묶어서 그룹을 만드는 기법
데이터가 문서일 때는 문서 클러스터링
같은 cluster에 있는 문서들은 서로 비슷하고, 다른 cluster에 있는 문서들은 서로 달라야함
비지도학습(Unsupervised Learning의 한 방법 → 즉, label이 없는 상태)
Similarity
문서 clustering에서 비슷한 문서끼리 묶는다고 했을 때, 비슷함은 무엇을 기준으로 잡을까?
→ vetor space에서 가까운 거리에 있는 것들! (Euclidean Distance)
→ 확률적으로 비슷한 단어들이 많이 발생하는 문서들
K-means clustering
간단하면서도 성능이 좋은 대표적인 clustering 방법론으로, 각 cluster는 cluster centroid와 그 cluster에 속하는 data sample들로 구성됨
cluster centroid로부터 그 cluster에 속하는 샘플들의 거리의 합이 최소가 되도록 cluster를 조정해 나감 (즉, 계속 값을 바꾼다.)
cluster를 조정한다는 것은, cluster centroid의 위치와 각 cluster에 속하는 sample들을 바꾸어 나간다는 뜻!
K-means clustering의 결과는 K의 개수와 초기 seeds에 많이 좌우됨 (대부분의 경우 K는 미리 정해짐)
Euclidean distance가 아닌 다른 종류의 distance(Manhattan, maximum, Mahalanobis…)도 사용가능함
- input: 문서집합, cluster의 개수 K (K: 미리 정해놓음)
- output: 각 cluster에 할당된 문서들
- Algorithm
step1 : K개의 문서를 임의로 선택 (seeds, 임의로 선택한 점이 임시의 centroid가 됨)
step2: 각 문서에 대해 가장 가까운 seed를 선택하여 할당
step3: K개의 centroid를 계산 (해당 cluster에 포함된 모든 문서들의 평균)
step4: 각각의 문서를 다시 가까운 centroid에 할당(update!)
step5: K개의 centroid를 다시 계산
step 4,5를 반복 (종료조건을 만족할 때까지! 즉, 더 이상 centroid가 변하지 않으면 clustering을 멈춤 & 계속 바뀌어서 멈추지 않는다면 n번 후에 stop하는 종료조건을 줄 수 있음)
Hierarchical Clustering
Hierarchical clustering(계층적 군집)은 cluster의 계층을 만드는 clustering 방법이다.
아래는 clustering 방법들로, 결국 비슷하다는 것(similarity)에 대한 기준이 있어야 하므로 data sample의 distance를 사용하여 계산한다.
- Agglomerative clustering(병합군집)
‘Bottom up’형식으로, 각 data sample로부터 출발하여 가까운 cluster들이 합쳐지는 형식으로 cluster가 만들어진다.
- Division clustering(분할군집)
‘Top down’형식으로, 모든 data sample들이 처음에는 한 cluster에 있다가 점점 분할되면서 cluster들이 만들어진다.
Agglomerative Clustering Types (대표값을 정하는 방법)
Single Link(nearest neighbor) vs Complete Link(diameter)
- Single Link: 두 개의 cluster의 similarity가 가장 가까운 점들끼리로 정해짐. cluster의 전체 구성을 보는 것이 아닌 일부 지역으로 판단하므로 noise, outliers에 민감하다.
- Complete Link: 두 개의 cluster의 similarity가 가장 먼 점들끼리로 정해지므로, 지름이 가장 작은 cluster를 만들게 된다(→ 응집이 잘 된 cluster를 찾음). 지역적으로 판단하는 것이 아니라 전체를 판단하는 것이므로 소규모의 cluster를 찾게 되며, outliers에 민감하다.
Average Link(group average) vs Centroid Link(centroid similarity)
- Average Link: 두 개의 cluster의 similarity가 거리의 평균으로 계산됨. 즉, 한 cluster와 다른 cluster에서 각각 점을 하나씩 뽑아서 쌍을 만들고 모든 가능한 쌍에 대해서 거리를 계산하고 평균함.
- Centroid Link: 두 개 cluster의 similarity가 centroid(중심)으로 계산됨 (→ 각 cluster에서 중심점을 찾아서 그것으로 계산!)
실루엣 계수(Silhouette Coefficient)
각 데이터 포인트와 주위 데이터 포인트들과의 거리 계산을 통해 값을 구하며, cluster 안에 있는 데이터들은 잘 모여있는지, cluster끼리는 서로 잘 구분되는지 clustering을 평가하는 척도로 활용한다. 군집 내 비유사성(within dissimilarities)는 작고, 군집 간 비유사성(between dissimilarities)는 커야 clustering이 잘 되었다고 할 수 있다. 실루엣 계수를 구하는 방식은 아래의 식과 같다.
- a(i) : data point ‘i’가 속한 cluster 내의 data point들과의 거리 평균
- b(i) : data point ‘i’가 속하지 않은 cluster 내의 data point들과의 거리 평균
- 모든 data point 들에 대해 s(i)를 계산한 후, s들의 평균값(overall average silhouette width)을 계산한다.
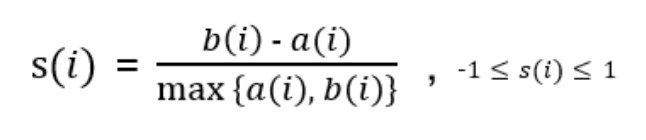
cluster 개수별로 여러 번 clustering을 했거나, 여러 기법을 이용해서 clustering한 경우 s의 평균값을 비교하여 cluster 개수를 몇 개로 할 것인지, 어떤 cluster 기법을 선택할 것인지 판단할 수 있다. 실루엣 계수(s)의 평균값이 1에 가까울 수록 clustering이 잘 된 것이다. (0에 가까운 값이면 → weak cluster)
만약 100개의 data point(i)가 있다면 99개의 다른 data point들과 거리를 구해서 s를 계산하고, 이런 동일한 연산을 100번 수행해야하므로, 데이터 양이 많아질수록 수행 시간이 매우 오래 걸린다.
[Practice] Silhouette Coefficient 계산하여, 적절한 k값 찾기
Uploaded by N2T


