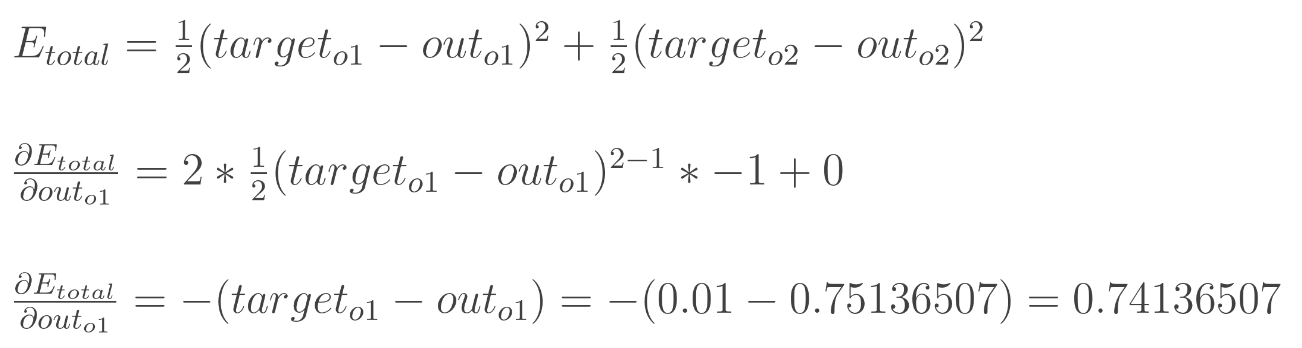Backpropagation
오차 역전파법으로 해석되는 backpropagation은 neural network를 학습하기 위한 방법이다.
Neural Network에서 계산한 결과와 실제 결과의 차이를 식으로 만들고, 이를 최소화하는 최적화 문제를 풀게된다.
- 일단 input을 넣어서 계산해보고(Forward Propagation)
- 계산된 값과 실제값의 차이를 계산한 뒤
- Backpropagation(Backward Propagation)으로 parameter를 업데이트
Backpropagation algorithm
- Step1 : propagation → 네트워크에 input을 넣어서 output을 계산하고, 출력과 실제값의 차이를 계산(cost)
- Step2 : backpropagation
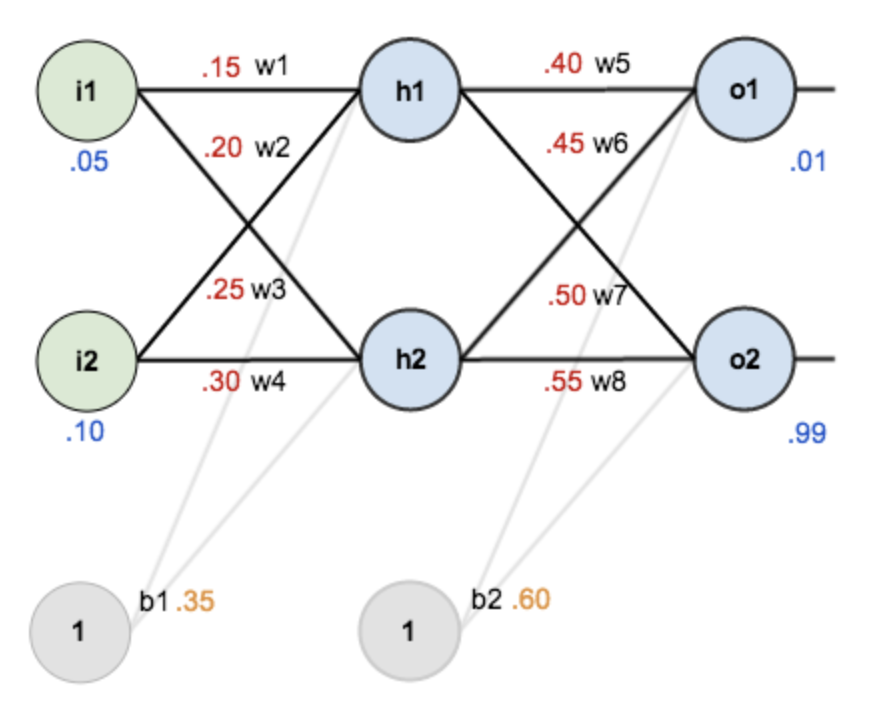
입력 feature 개수(2) / hidden layer(1) / hidden neuron개수(2) / 출력 neuron개수(2)
Initial value 할당
- initial weights(w), bias(b)를 랜덤으로 발생시켜서 셋팅
- training inputs(i), outputs(o)을 준비 → input 값 하나에 대해 예측하는 것을 살펴보도록 하자
The Forward Pass
할당된 initial value를 이용하여 input(0.05, 0.10)에 대해 예측을 수행해 본다
각 Node에는 activation function(활성화 함수)이 존재하며 sigmoid function을 적용한다.
- h1 노드에 대해 계산해보자
- sigmoid function을 activation function으로 적용
- h2 노드에 대해서도 마찬가지로 계산 → out(h2) = 0.596884378
- output node 인 o1에 대해서 계산해보자
- o2도 마찬가지로 계산 → out(o2) = 0.772928465
- 전체 에러는 다음과 같다
- Error Calculate (E(02)도 마찬가지로 계산 → 0.023450026)
- 위에서 구한 값들로 계산한 total error for the neural network
The Backwards Pass
backpropagation의 목적은 계산된 출력값(output)이 실제 출력값(target output)과 가까워지도록 weights를 update하는 것이다. (즉, minimize error가 목적)
w5의 경우, w5가 변화함에 따라서 error가 변화하는 정도를 알아야 한다 → 편미분
Chain Rule을 적용해서 계산한다.
- Node o1에 대해서 계산해보자. 출력값(out_o1)에 대한 에러(E_total)의 변화는?
- net input(net_o1)에 대한 출력값(out_o1)의 변화는?
- 마지막으로, w5에 대한 o1 net input(net_o1)의 변화는?
- 위에서 계산된 값들을 모두 곱하면, 구하고자 하는 편미분 값이 계산됨!
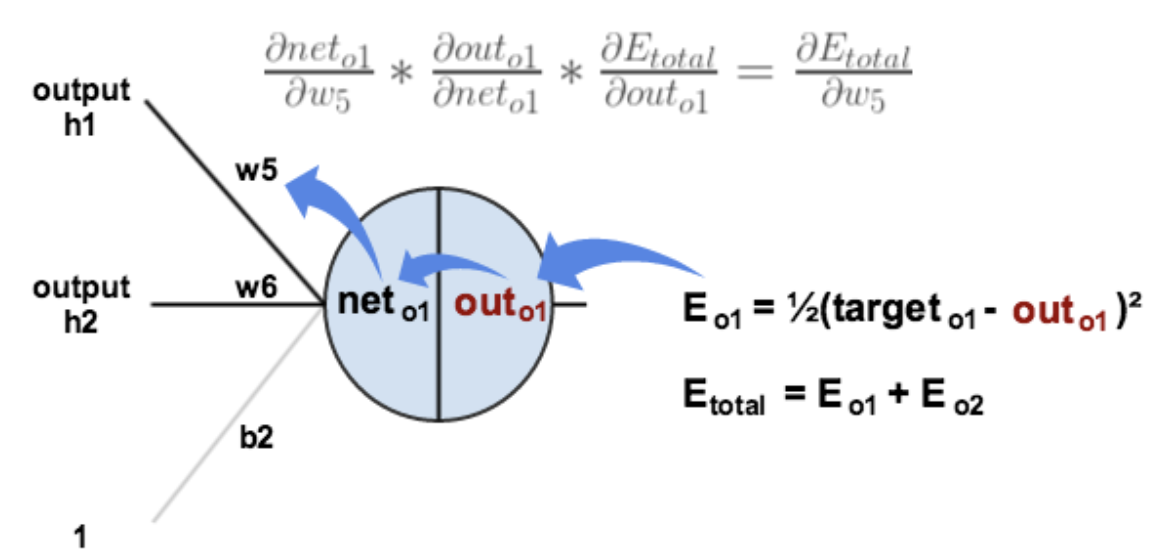
- 그리고, 결국 error를 감소시키기 위해서 현재 weight 값으로부터 위에서 계산된 값을 빼준다. (optionally multiplied by some learning rate, eta, which we’ll set to 0.5)
- 위와 같은 방법으로 다른 weights(w6+, w7+, w8+)를 update 한다.
Hidden Layer
이제, hidden layer에 해당하는 w1, w2, w3, w4에 대해서 계산할 차례이다.
우리가 필요로 하는 것은,
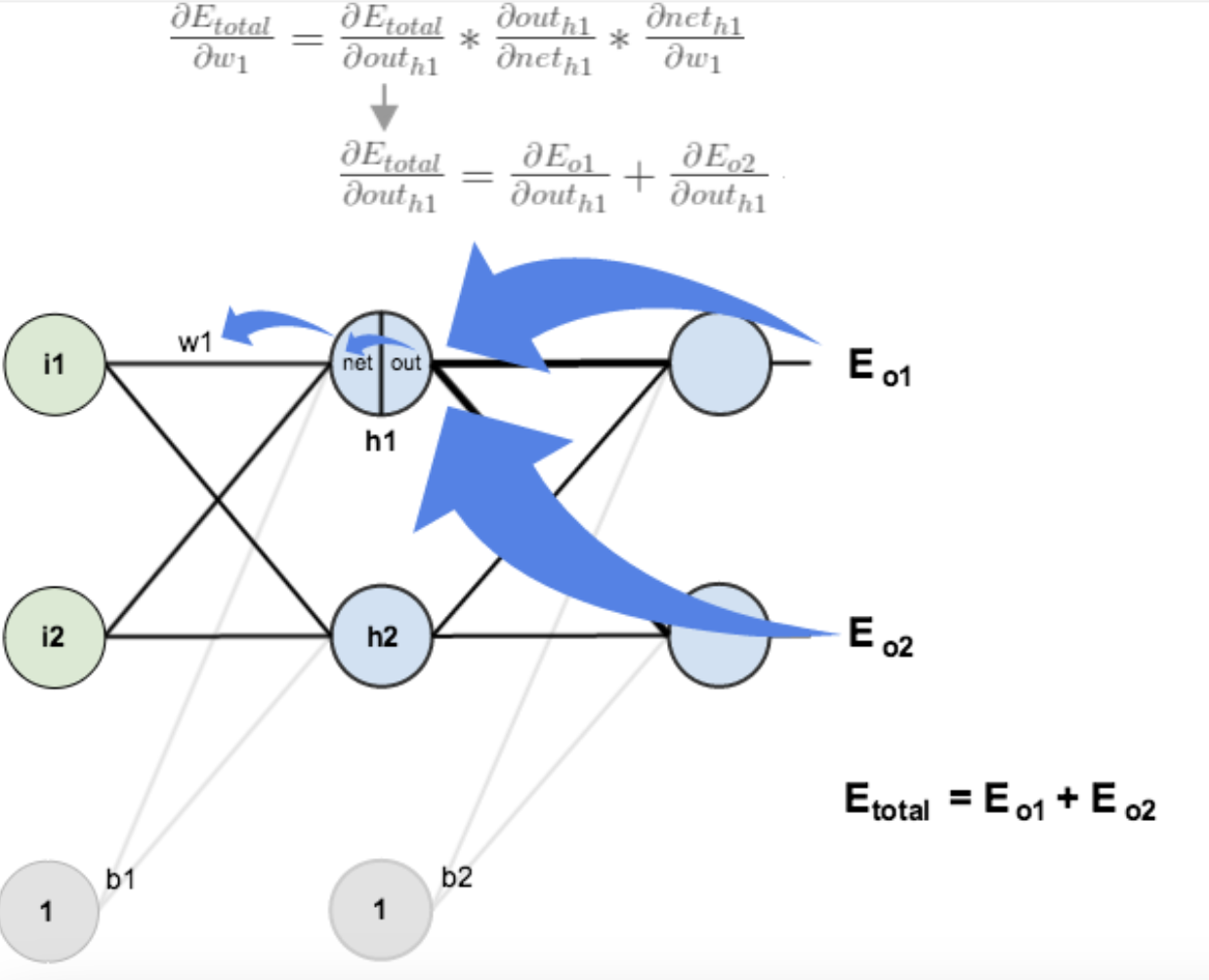
Output layer에서의 계산과 거의 비슷하지만 약간 다르다. (Hidden layer 뉴런 하나가 여러 개의 output 뉴런의 에러에 영향을 미침)
따라서 두 output 뉴런에서의 에러(E_o1, E_o2)를 모두 고려해야 함!
- E_o1부터 계산해보자 (E_o1을 계산하면 → -0.019049119)
- 아래 식에서 우변의 첫번째 항만 구했으므로, 나머지 값을 계산해야 한다.
- 나머지 값들을 각각 구해보자
- 구한 값들을 원래 식에 대입하면 최종적으로 아래의 값을 얻는다. → w1이 total error에 미치는 영향
- 최종적으로 w1을 update 한다. (같은 방법으로 w2, w3, w4도 업데이트!)
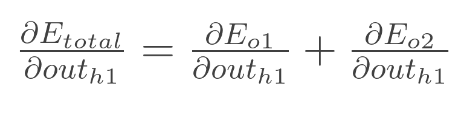
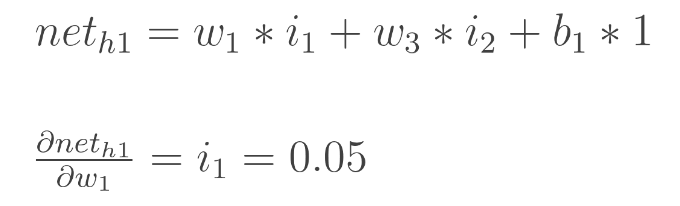
결과
업데이트 후에 input(0.05, 0.1)에 대해서 forward pass를 또 수행하면, total error가 0.2910…가 됨
업데이트 전에는 0.2983… 으로, error가 줄어들었다는 사실을 확인할 수 있음
적은 양이지만, training sample 한 개에 해당하는 error 이므로, 이를 계속 반복했을 때 error는 0에 가까워짐
Uploaded by N2T