| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- TFX
- SOMs
- Logistic Regression
- stemming
- 경사하강법
- textmining
- Generative model
- RNN
- 자기조직화지도
- ResNet
- NER
- tensorflow
- Clustering
- Binary classification
- Transfer Learning
- AI 윤리
- Ann
- cross domain
- nlp
- Python
- MLOps
- NMF
- VGGNet
- BERT
- Gradient Descent
- Support Vector Machine
- LSTM
- gaze estimation
- Attention
- 군집화
- Today
- Total
juooo1117
[Module 3] Machine Learning 개론: Bias and Variance 본문
[Module 3] Machine Learning 개론: Bias and Variance
Hyo__ni 2024. 1. 7. 12:38Part 2. Bias and Variance
Generalization in ML
기계학습 알고리즘의 능력을 말한다.
An ML model's ability to perform well on new unseen data rather than just the data that it was trained on.
→ 학습과정에서 보지 못한 새로운 data에 대해서 잘 하는 것이 더 중요하다.
Learning algorithm maximizes accuracy on training examples.
Strongly related to the concept of overfitting. (*overfitting = poor generalization)

*New unseen data에 대한 일반화 능력을 좀 더 높이기 위해서 accuracy를 낮추는 학습을 진행했다.
Training Data vs Test Data
- Universal set : 세상의 모든 개,고양이의 이미지 → 관측이 불가능한 data
- Training set : 개1000장, 고양이1000장 → 즉, universal set에서 sampling된 이미지
- Test set : training set과 마찬가지로 universal set에서 sampling 된 이미지이지만, training set과의 overlap은 없다.

Generalization Error
Objective of learning
- Not to learn an exact representation of the training data itself
- To build a statistical model that generates the data
True Distribution : P(x,y)
- All possible cases - unknown to us
- Train and test data are generated by P(x,y)
- Assumption : iid (independent and identically distributed)
Train : Fit a hypothesis h(x)
- Using training data S → True distribution으로부터 N개의 data를 sample한 것이 학습 data S로 주어진 상황
Underfitting : Generalization error < Training error (the training error is not sufficiently low)
Overfitting : Generalization error > Training error (the gap between the training and test error is too large)
*underfitting이 생겼다는 것은 학습조차 제대로 시키지 못했다는 것!
Training an ML algorithm well
- Make the training error small (일단 overfitting이 발생할 때까지 학습데이터로 학습을 잘 시킨다)
- Make the gap between the training and test error small (overfitting을 낮추는 방법을 찾는다)
Typical Relation between Capacity and Error
Informally, a capacity is the function's ability to fit a wide variety of functions.
As capacity increases, training errors decreases but the gap increases
(training error: 측정가능 / generalization error: 측정 불가능, 따라서 validation error등으로 예측만 가능!)
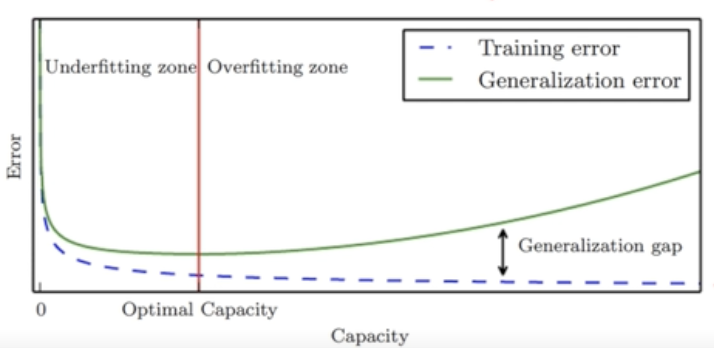
Model의 Capacity를 높이면 높일수록 무조건 training error는 줄어든다.
training error를 줄이고 싶다면 계속 model의 복잡도를 높이면 된다. → 하지만 우리는 generalization error를 줄이는 것이 목적!
따라서, green line이 최소화되는 지점을 찾아야 한다.
Regularization
Given an ML algorithm, a preference for one solution in its hypothesis space to another
- parameter : 학습을 통해서 배우는 변수
- hyper-parameter : 우리가 주어야 되는 parameter (*lambda)

lambda를 작게주면 첫 번째 term을 더 고려를 많이 하겠다는 것이다.
Hyperparameter, tuning parameter는 cross validation(교차검증) 과정을 통해서 결정하게 된다.
The main objective of regularization is to reduce its generalization error but not its training error.
(training error를 낮추는 것이 아니라, regularization error를 낮추는 것이 목적이다)
→ training error를 낮추고 싶으면 regularization 을 전혀 안 쓰는 것이 무조건 좋다.
Bias/Variance Decomposition
최적의 ML model을 찾아가는데 가장 중요한 개념이다.
올바르게 Prediction 하려면 low-bias(predicted well) & low-variance(stable) 가 필요하다.

Trade-off between Bias and Variance
Two sources of error in an estimator : bias and variance
- Bias : Expected deviation from the true value of the function (예측값에 대한 평균과 true 와의 차이)
- Variance = Deviation from the expected estimator values obtained from the different sampling of the data
→ Generalization 혹은 Test error = Bias + Variance
따라서, Bias와 Variance를 낮추는 게 우리의 목표가 된다.
하지만 Bias - Variance 사이에는 trade-off 관계가 존재한다.
Overfitting vs Underfitting
High variance implies overfitting
- Model class unstable
- Variance increases with model complexity
- Variance reduces with more training data
High Bias implies underfitting
- Even with no variance, model class has high error
- Bias decreases with model complexity (모델의 복잡도가 너무 낮아서 좀 허접한 모델이다.)
- Independent of training data size
'Artificial Intelligence > LG Aimers: AI전문가과정' 카테고리의 다른 글
| [Module 4] Supervised Learning: Linear Regression Model (2) | 2024.01.09 |
|---|---|
| [Module 3] Machine Learning 개론: Recent Progress of Large Language Models (1) | 2024.01.07 |
| [Module 3] Machine Learning 개론: Introduction to ML (0) | 2024.01.06 |
| [Module 2] Mathematics for ML: PCA (0) | 2024.01.06 |
| [Module 2] Mathematics for ML: Convex Optimization (0) | 2024.01.06 |




