Linear model (Regression)
학습을 통한 예측
- 목적: 집 크기에 대한 함수를 써서 집 값을 예측하는 것
- 이 때, 함수(h)를 hypothesis(가설)이라고 함
- 가설은 모수(parameters)를 사용하여 표현됨 → 학습 알고리즘을 통해 학습 집합에 가장 맞는 가설 h(θ)을 찾아냄
- 새로운 데이터가 주어지면 y값을 예측할 수 있음
Linear Regression
선형회귀: 수치 데이터를 예측하기 위한 기초적인 방법
- 결과값이 입력된 속성값들(attribute values)의 선형 조합(linear combination)이다.💡𝑦 = 𝑤0 + 𝑤1𝑥1 + 𝑤2𝑥2 + ... + 𝑤n𝑥n (input → n dimension) (𝑦: result / 𝑥1, ... , 𝑥n : attribute values / 𝑤0, 𝑤1, ... , 𝑤n : weights)
- 기계학습에서는 회귀(regression) 문제를 실수 예측 문제로 간주한다.
- 학습 집합으로부터 weights( → 가중치, 모수)가 계산됨 (학습 데이터를 통해서 weights 결정!)💡𝐷(학습집합) = {(x(1), 𝑦(1)), (x(2), 𝑦(2)), ... , (x(m), 𝑦(m))}
**(m개의 데이터가 쌍으로 존재, input-output)
x(m) = (𝑥(1)(m), 𝑥(2)(m), ... , 𝑥(n)(m))
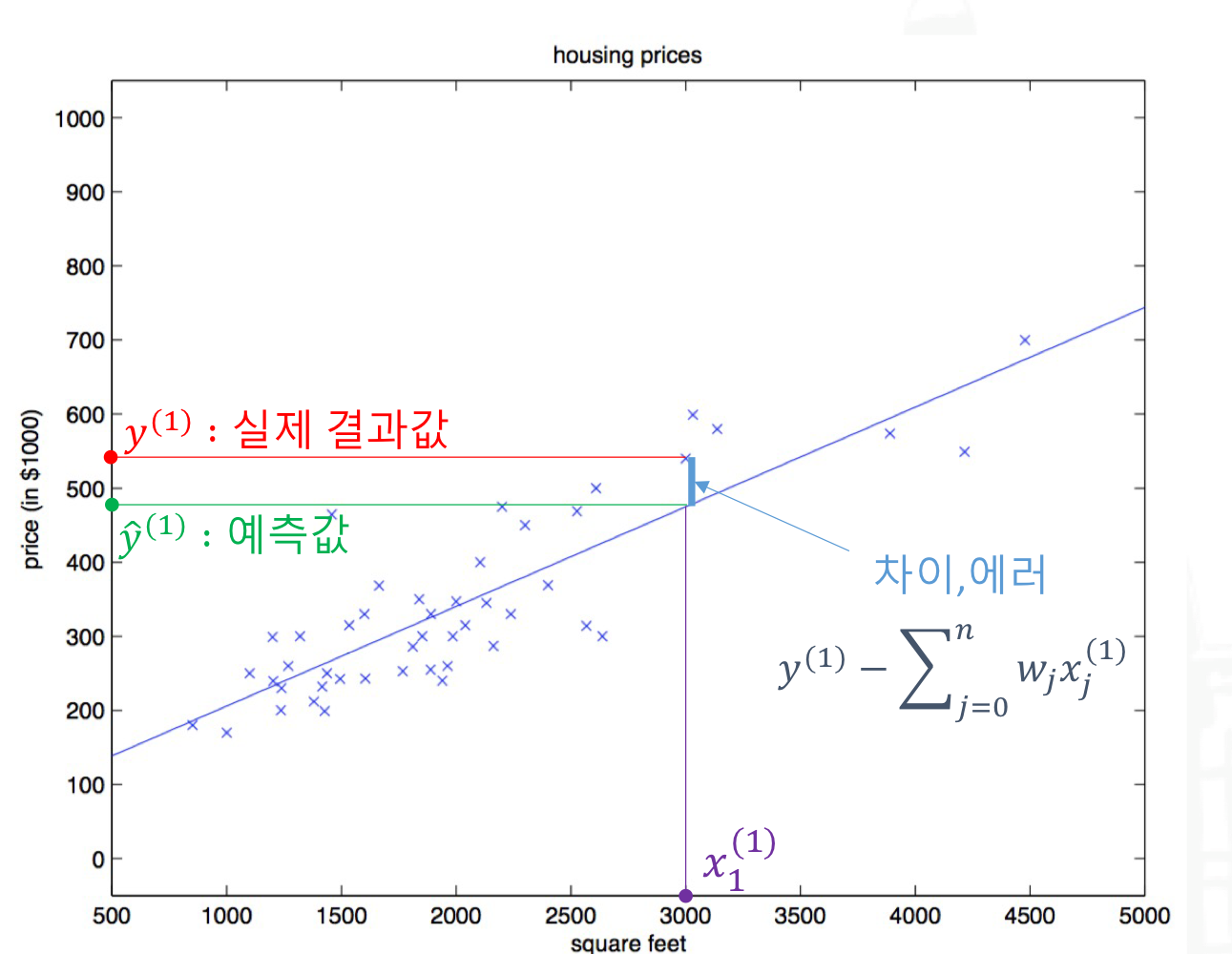
- weights값을 잘 구해서 예측값이 실제 결과값과 비슷하도록 해야한다.
→ 학습 데이터로부터 패턴을 찾음
→ 에러(실제 결과값과의 차이)를 계산해서, 그 에러가 최소가 될 수 있는 계수들을 구한다.
→ 실제 결과값과 예측값의 차이를 수식화해서 이를 최소화하는 weight를 구한다.
→ 즉, 선형회귀모델에 가장 잘맞는 직선을 만들 수 있도록 error를 없애자
Mean Squared Error
error를 어떻게 최소화할 것인가? → 일단 error를 수식으로 표현할 수 있어야 한다.
MSE 수식: (m: data sample, i: i번째 sample, w: 구해야 하는 값)
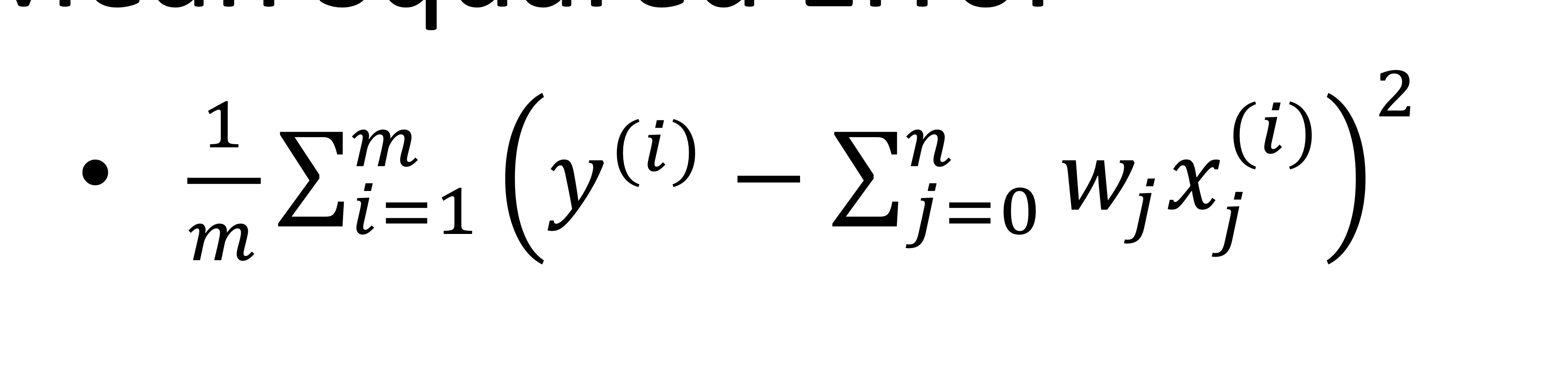
- 위의 에러를 최소화하는 계수들을 구함 (학습데이터 대입)
- cost funciton(비용함수)라고도 함 → cost(W)
- W에 대한 함수로 생각할 수 있음 (W에 대한 제곱형태)
Optimization - Gradient Descent
error를 줄이기 위해서, 최적화문제로 생각하고 ‘gradient descent’ 등의 최적화 알고리즘을 이용하여 W를 구한다.
계속 W를 업데이트하는 과정을 학습(training)이라고 함 (alpha : step size 결정계수 → 너무 급작스럽게 변하지 않게 해줌)
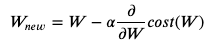
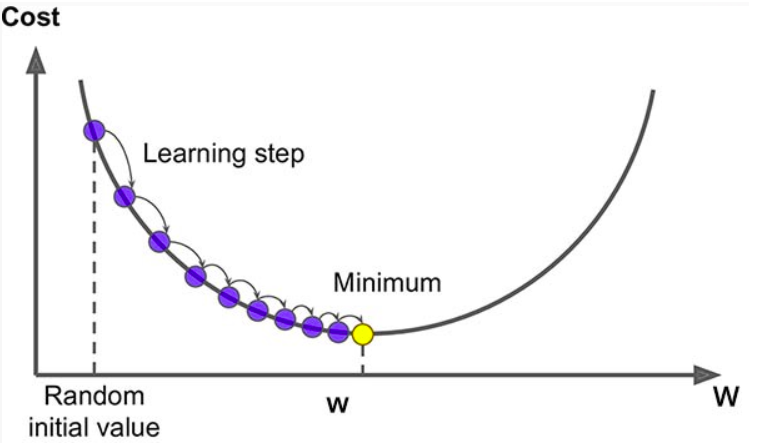
- 임의의 값(random initial value) w에서 출발 → minimize되는 최저점(error가 가장적음)을 찾아야 함
- 기울기를 찾아서 기울기의 반대방향( -, negative)으로 기울기만큼 update!
- Final Goal : Cost function의 minimize
Gradient Descent & Cost Function
Gradient Descent:
1차 근삿값 발견용 최적화 알고리즘이며, 기본 개념은 미분을 이용하여 함수의 기울기(경사)를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동시켜 극값에 이를 때까지 반복하는 것이다. → to find solution with min error
parameter에 대해 기울기를 계산하여 이동할 방향(기울기의 반대로 감)을 결정
Cost Function:
parameters에 대한 convex(볼록) 함수. 수식으로 예측한 결과와 실제 값의 차이를 말한다.
- 왼쪽그림: 이런 모양이 나와야 linear regression에서 optimal value를 얻을 수 있다.
- 오른쪽그림: 그래프가 울퉁불퉁하면 local minimum에 빠진다.
Linear Models for Classification
어떤 종류의 Regression 기술도 Classification으로 사용될 수 있음
학습 시, Regression을 각 class에 대해서 수행함. 그 class에 속하면 ouput=1, 그렇지 않으면 output=0 이다.
결과값은 [0, 1] 사이가 아닐 수 있으므로, 확률 기반의 예측이 아니다.
Multiclass Classification:
- 각각의 class를 학습 후 특정 instance(sample)의 class를 예측 시, 그 값이 가장 높은 class를 선택하여 예측함
- 고양이, 개, 토끼 분류에서는 “고양이다/아니다, 개이다/아니다, 토끼이다/아니다”와 같이 각각의 모델을 만듦
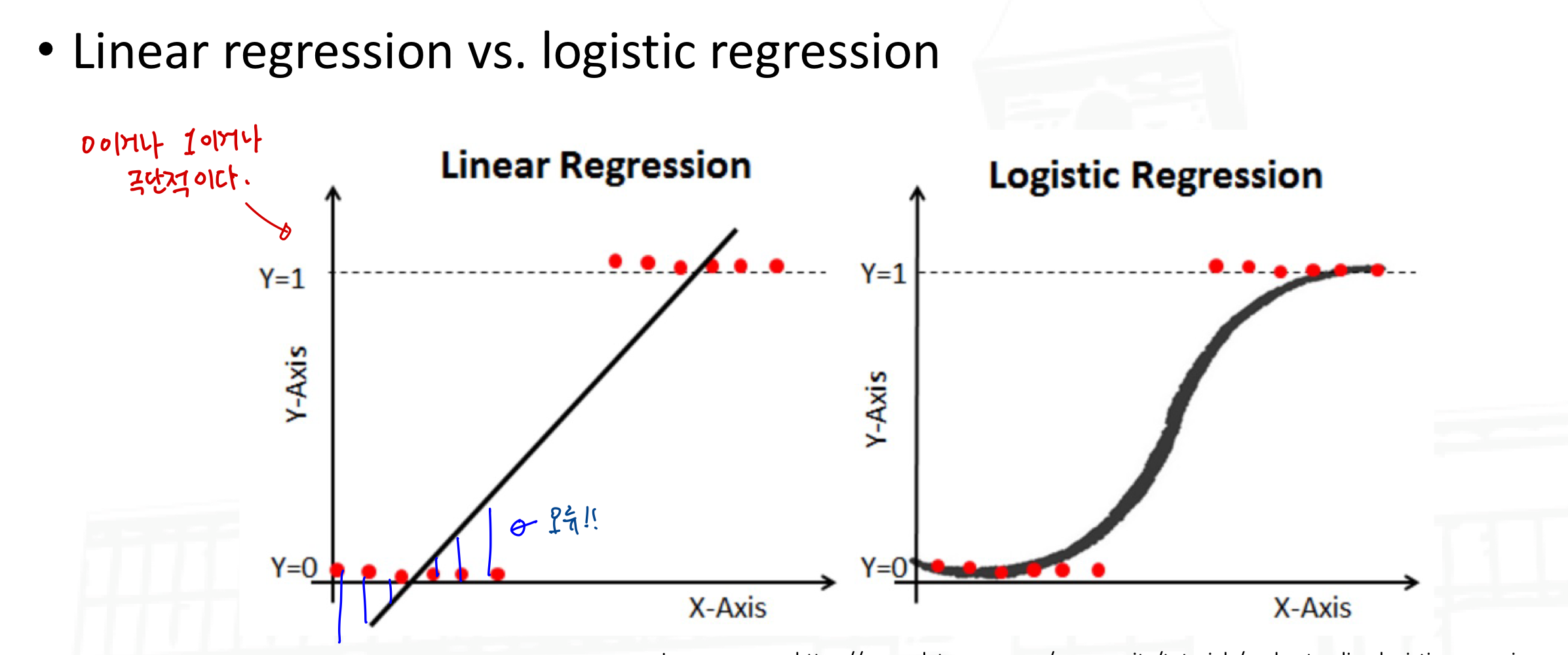
Logistic Regression:
Classification에 사용됨 → 두 개의 class에 대해서 수행함 (label 1 or lable 2)

linear regression에 비해서 logistic regression은 오류의 차이가 크지 않다.
Uploaded by N2T

